Gráfico de pastel

04 de marzo del 2013.
Unidad: Estadística.
Séptimo grado.
Contenido:Gráfico de Pastel

Ø  Gráfico de pastel o de sectores.

En este tipo de gráfico,  lo que vamos a comparar es la amplitud de los sectores circulares que, para cada uno de los datos, vamos a dibujar sobre un mismo círculo. Son útiles para comparar datos pues, en general, trabajan con porcentuales, el área de cada sector representa el porcentaje que corresponde a la frecuencia de un cierto valor de la variable, esta representación es conveniente cuando el número de sectores es pequeño y sus áreas están bien diferenciadas.

El motivo de un gráfico de pastel  es representar las frecuencias en forma de sectores circulares. El tamaño de los ángulos de estos sectores ha de ser directamente proporcional a las frecuencias.

Podemos empezar con la creación de una tabla de frecuencia  como la de abajo. En la última columna hemos puesto la frecuencia total y el total de grados que cubre una circunferencia completa, es decir 360º.

 Ejemplo: Resultados de una muestra de  las calificaciones finales en Matemáticas de Sexto grado de una escuela de Fe y Alegría.

Categoría	Frecuencia	Frecuencia Porcentual F%	Procedimiento
Aprendizaje Inicial ( AI)	2	( 2 x 100) ÷ 52 = 4 %	4 % = 0.04 x 360 =  14º
Aprendizaje Elemental ( AE)	24	( 24 x 100) ÷ 52 = 46%	46%= 0.46 x 360 = 166º
Aprendizaje Satisfactorio (AS)	10	( 10 x 100) ÷ 52 = 19 %	19%= 0.19 x 360 =  68º
Aprendizaje Alcanzado (AA)	16	( 16 x 100) ÷ 52 = 31 %	31%= 0.31 x 360 = 112º
Total	52	( 52  x 100) ÷ 52 = 100 %	Total 100%=  1 x 360 =  360º

Ahora podemos dibujar (con ayuda del transportador y compás) un gráfico de sectores como el de abajo.

Resultado por categorías

Con la siguiente información construye gráficos de pastel

1. Candidatos a la presidencia escolar en el colegio.

Nombre del candidato Frecuencia absoluta Porcentajes Carlos 6 Paula 8 Carmen 5 Ana 3

2. Tome dos de las tablas de frecuencias que ha construido en su cuaderno y elabore gráficos de pastel con estos datos.

ECUACIONES CUADRATICAS

Fecha: 19 de noviembre del 2012

 VII UNIDAD: FUNCIONES Y ECUACIONES.
CONTENIDO:
                          Ecuaciones cuadráticas.

TEOREMA DE PITÁGORAS

TEOREMA DE PITÁGORAS

 

	En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. a2 + b2 = c2
Cada uno de los sumandos, representa el área de un cuadrado de lado, a, b, c. Con lo que la expresión anterior, en términos de áreas se expresa en la forma siguiente:
El área del cuadrado construido sobre la hipotenusa de un triángulo rectángulo, es igual a la suma de las áreas de los cuadrados construidos sobre los catetos.

Teorema de Pitágoras generalizado

Si en vez de construir un cuadrado, sobre cada uno de los lados de un triángulo rectángulo, construimos otra figura, ¿seguirá siendo cierto, que el área de la figura construida sobre la hipotenusa es igual a la suma de las áreas de las figuras semejantes construidas sobre los catetos?

(Pinchando en los dibujos siguientes se accede a la comprobación numérica en las figuras que se representan)

Aplicaciones del teorema de Pitágoras.

Analice los siguientes ejercicios resueltos, si tiene dificultades no dude en preguntar.

1. Una escalera de 10 m de longitud está apoyada sobre la pared. El pie de la escalera dista 6 m de la pared. ¿Qué altura alcanza la escalera sobre la pared?

 

La escalera sobre la pared alcanza una altura de 8 metros.

 Abrir los documentos en PDF que estan en escritorio para realizar las actividades propuestas...

TEOREMA DE LOS CATETOS Y LA ALTURA

 Fecha:  22-10-2012

VI UNIDAD: Congruencia y semejanza de triangulos.

Contenido:

Teorema de los catetos.

Teorema de la altura.

"Hola chicos" hoy trabajaremos dos teoremas muy importantes, recordemos que hay que leer y analizar, tratemos de no dedicarnos unicamente a copiar, yo se que todos tienen grandes capacidades, si tienes dificultades en el análisis puedes llamarme...

"MUCHA SUERTE Y MANOS A LA OBRA".

Teorema de los catetos.

En todo triángulo rectángulo un cateto es media proporcional entre la hipotenusa y su proyección sobre ella.

a hipotenusa

b y c catetos

m proyección del cateto b sobre la hipotenusa

n proyección del cateto c sobre la hipotenusa

Ejemplo 1.

La hipotenusa de un triángulo rectángulo mide 30 cm y la proyección de un cateto sobre ella 10.8 cm. Hallar el otro cateto.

Teorema de la altura. 

En un triángulo rectángulo, la altura relativa a la hipotenusa es media proporcional entre los 2 segmentos que dividen a ésta.

En un triángulo rectángulo, las proyecciones de los catetos sobre la hipotenusa miden 4 y 9 metros. Calcular la altura relativa a la hipotenusa.

  Ejemplo 1:

 Vendo un genial celular con tapita de última oferta, no se quede sin el suyo es un excelente teléfono.

 
 

Sistemas de ecuaciones lineales

SISTEMAS DE ECUACIONES LINEALES CON DOS VARIABLES. 

Un sistema de ecuaciones con dos incognitas (variables) es un sistema lineal  de ecuaciones formado por dos ecuaciones que admiten un tratamiento especial para su solución tienen la forma:
 donde  a,b,c,d,r  y  s, son constantes.

El conjunto solución de un sistema de ecuaciones lineales en dos variables es el conjunto de todos los pares ordenados que satisfacen las dos ecuaciones del sistema.

Al resolver un sistema  de ecuaciones lineales en dos variables tenemos una de estas tres posibilidades como solución:

• una solución única, esto es, que las rectas se intersecan en un punto.  En este caso, se dice que el sistema es independiente.  Ejemplo:

Las rectas tienen pendientes diferentes.

• ninguna solución, esto es, que las rectas son paralelas.   El sistema es inconsistente.     Ejemplo:

Las rectas tienen la misma pendiente pero los interceptos en y son diferentes.

• infinito número de soluciones, esto es, que las rectas coinciden.  El sistema es dependiente.  Ejemplo:

Las rectas tienen la misma pendiente y el mismo intercepto en y.

En la próxima clase aprenderemos a identificar cada uno de estos casos tomando en cuenta el tipo de sistema con el que trabajemos.

SOLUCION DE UN SISTEMA DE ECUACIONES.

Aprederemos a resolver sistemas de ecuaciones pot diferentes metodos la correcta aplicanción de ellos estara en depenencia del grado de atención que pongas, iniciaremos estudiando el metodo de REDUCCIÓN O METODO DE SUMA Y RESTA.

• Método de reducción

  Combinación lineal de ecuaciones : se multiplica una ecuación por ún número, la otra por otro número y se suman. La ecuación resultante de una combinación lineal es equivalente a las ecuaciones originales del sistema.
  El método de reducción consiste en eliminar una incognita del sistema.
  
  
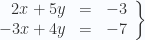
  1. Vamos a eliminar la . Para ello multiplico la ecuación de arriba por 3 y la de abajo por 2:
     
  2. Sumando ambas ecuaciones desapacen las x y nos queda
     
     
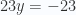
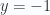
  3. Para calcular x sustituimos en cualquiera de las ecuaciones originales. Sustituyendo en la primera nos queda
     
     
     

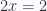
  Leer y analizar el siguiente problema:

Entre Ana y Sergio tienen 600 cordobas, pero Sergio tiene el doble de dinero que Ana. ¿Cuánto dinero tiene cada uno?.

Llamemos "x" a la cantidad de cordobas de Ana e "y" a la cantidad de cordobas de Sergio. Vamos a expresar las condiciones del problema mediante ecuaciones: Si los dos tienen 600 cordobas, esto nos proporciona la ecuación x + y = 600. Si Sergio tiene el doble de dinero que Ana, tendremos que y = 2x. Ambas ecuaciones juntas forman el siguiente sistema:

   x + y = 600
2x - y = 0

Vamos a resolver el sistema por el método de reducción. Para ello, teniendo en cuenta que, en ambas ecuaciones, la "y" tiene coeficientes opuestos, podemos pasar a sumar directamente ambas y nos quedará:

3x = 600 ⇒ x = 600/3 ⇒ x = 200

 Sustituimos la x para despejar la "y", y tenemos:

200 + y = 600 

 y = 600 - 200

y = 400 

  Por tanto, la solución al problema planteado es que Ana tiene 200 cordobas y Sergio tiene 400 cordobas.

 Ejercicios para resolver en parejas:

  1. Resolver los siguiente sistemas de ecuaciones lineales:

A.   2X-Y=1        B.  X-Y=0        C.  -X+4Y=-1
      X+Y=0            X+Y=1            2X-3Y=0

  1. Resolver los siguiente sistemas de ecuaciones lineales:

A    X+Y=0           B   X+Y=0        C.   X-2Y=1
    2X+2Y=4              2X+2Y=0         -2X+4Y=-2

 3. ¿De cuáles de estos sistemas es solución el par x = 1, y = -3

4. Escribe otro sistema que tenga la misma solución. 

2. Completa los siguientes sistemas para que la solución de todos ellos sea:
   
   x = 2
   y = -1
   
   

1. Un grupo de amigos tuyos alquila una casa rural para pasar un "puente". Le preguntan al dueño si hay animales en la casa, cuántos y de qué tipo. El dueño, dándoselas de "gracioso" delante de los, según él, tontos de la capital les responde:
   "Tenemos 22 cabezas y 70 patas entre conejos y pájaros".
   Ayuda a tus amigos para que no queden como "pardillos" y averigüa cuántos conejos y cuántos pájaros hay en la casa que han alquilado.
   

 Resolver los siguientes sistemas por el metodo de REDUCCION.

 Actividades tomadas de: http://thales.cica.es/rd/Recursos/rd99/ed99-0045-01/secciones/reduccion.html